교통공학에서 최소곡선반경에 대해서 살펴보겠습니다.
최소곡선반경(Min. Radius of Circular Curve)은?
도로의 곡선 부분에서 차량의 주행 안전성을 확보하기 위해 설계속도의 기준에 따른 최소곡선반경을 의미합니다. 도로의 곡선 부분은 직선 부분과는 다르게 윈심력이 작용하기 때문에 이를 고려하여 최대한 직선 부분과 비슷한 주행 안전성을 유지하기 위해서 고려해야할 점이 많습니다. 그래서 차량이 안전하게 돌 수 있는 최소한의 곡선 반지름을 규정하고 차량이 밖으로 밀려나지 않기 위한 최소한의 편경사를 규정하게 됩니다. 그렇게 되면 횡방향 마찰력이 원심력보다 크게 되어 차량이 바깥으로 밀려나지 않고 안전하게 주행을 할 수 있습니다.
최소곡선반경의 공식은 다음과 같습니다.

※ 편경사: 평면 곡선부에서 차량이 원심력에 저항할 수 있도록 설치하는 횡단경사
※ 미끄럼 마찰계수
- 마찰계수는 0~1 사이의 값으로 표현, 0에 가까울수록 마찰이 적은 미끄러운 상태 의미
- 마찰계수에 영향을 주는 요소: 타이어 상태, 오면 습윤 상태, 도로 포장 재질 등
- 도로가 습윤하거나 타이어 마모가 심한 경우, 마찰 계수가 작아져 미끄러운 상태가 되어 위험이 커짐
위의 공식에서, 127은 단위 환산을 위해 나오게된 수 입니다. 위의 공식을 적용할 때, 주로 속도는 kph를, 거리는 m를 사용하기 때문에 편의상 위와 같이 표현된 것 입니다.
위의 공식이 어떻게 얻어지는지 증명을 해보겠습니다.
먼저 다음의 그림과 같이 차량이 평면 곡선 경사면을 주행하고 있다고 생각해봅니다.(곡선부 단면)

위의 상황에서 도로와 수평인 방향으로 힘의 평형을 식으로 나타내면 다음과 같습니다.
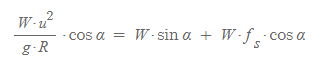

위의 식을 정리하면 다음과 같습니다.

그런 후 다시 정리하면 다음과 같이 나오게 됩니다.

tanα는 (편)경사도를 나타내는 것이기 때문에 편경사 e로 표시해도 무방합니다. 그리고 R의 단위는 m, u의 단위는 km/h, g=9.8m/s2이기 때문에 정리를 하면 다음과 같이 나오게 됩니다.

이때, 속도 u는 설계속도를 사용하면 됩니다.
[자료 출처]
- Professor Seungmo Kang, Korea University
- © 2009 Cengage Learning, Engineering
'교통공학' 카테고리의 다른 글
| 신호 교차로(Traffic Signalized Intersection)의 개념과 운영 방식 (0) | 2025.03.14 |
|---|---|
| 시공도 (Time-Space Diagram) (2) | 2024.07.01 |
| 평면 곡선(수평 곡선, Horizontal Curve) 2 (0) | 2023.07.23 |
| 평면 곡선(수평 곡선, Horizontal Curve) (0) | 2023.07.22 |
| 정지시거(Stop Sight Distance)와 판단시거(Decision Sight Distance) (0) | 2023.07.16 |



